OPERACIONES DE CONJUNTOS

Unión de Conjuntos

Sean A y B dos conjuntos. Se define la unión de A con B, denotada por (que se lee A unión B)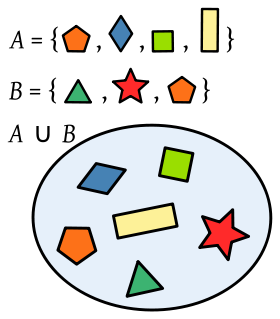

Intersección de Conjuntos

Sean A y B dos conjuntos. Se define la intersección de A y B, denotada por (que se lee A intersección B).

Ejemplo

A = { a, b, c, d, e} 

B = { a, e, i, o}

la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es:

A 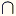B = { a, e}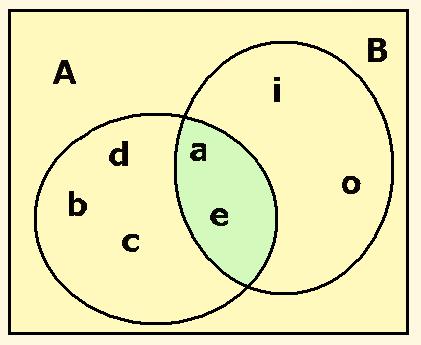 

Diferencia de Conjuntos

Sean y dos conjuntos. Se define la diferencia de con , denotada por (que se lee A menos B). Que resulta en otro conjunto, cuyos elementos son todos aquellos en el primero de los conjuntos iniciales que no estén en el segundo.
 
DIFERENCIA SIMÉTRICA 

Es una operación que resulta en otro conjunto cuyos elementos son aquellos elementos no comunes entre A y B, se podría decir que la diferencia simétrica es la operación complementaria(contraria) a la intersección.pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez.











CONJUNTO COMPLEMENTARIO
Es otro conjunto que contiene a los conjuntos con sus respectivos elementos.